摆锤冲击试验计算公式,摆锤冲击试验计算公式解析与应用概述

摆锤冲击试验计算公式：一场关于能量与耐力的科学博弈

想象你手中握着一把精密的摆锤，它即将以雷霆万钧之势砸向一块材料。这不仅仅是一场简单的物理演示，而是一场关于能量转换与材料耐力的科学博弈。摆锤冲击试验，作为材料科学领域不可或缺的测试手段，通过模拟外力冲击，揭示材料在瞬间受力下的表现。而这一切的背后，隐藏着一个关键的数学公式——摆锤冲击试验计算公式。这个公式，如同一把钥匙，打开了理解材料强度与韧性的大门。今天，就让我们一起深入探索这个公式的奥秘，看看它是如何将看似简单的摆锤运动，转化为对材料性能的深刻洞察。

摆锤冲击试验：一场瞬间的力量较量

摆锤冲击试验，也称为艾氏冲击试验，是一种测量材料在冲击载荷作用下抵抗断裂能力的经典方法。试验的核心装置是一根可以自由摆动的摆锤，当摆锤从一定高度释放后，会以巨大的动能冲击试样，使其断裂。通过测量摆锤冲击前后的能量差，可以计算出材料的冲击吸收功，进而评估其韧性。

想象当摆锤以每小时数百公里的速度砸向试样时，材料内部会发生怎样的变化？原子间的键会怎样断裂？能量又会在哪些环节被吸收或释放？这些问题，都离不开摆锤冲击试验计算公式的帮助。这个公式，不仅能够量化材料的冲击性能，还能为我们揭示材料在极端条件下的行为规律。

能量守恒：摆锤冲击试验计算公式的理论基础

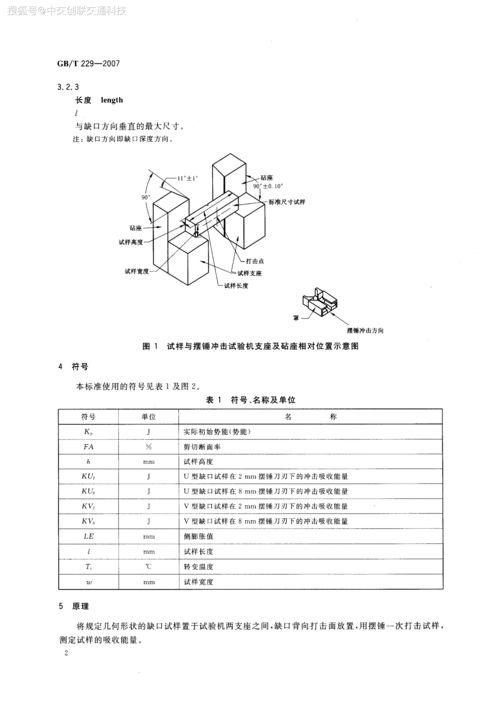
摆锤冲击试验计算公式的核心，是能量守恒定律。当摆锤从高处落下时，它具有势能，随着下落，势能逐渐转化为动能。冲击试样后，部分动能被试样吸收，导致摆锤的摆幅减小。通过测量摆锤冲击前后的摆幅，可以计算出试样吸收的能量。

这个过程中，能量守恒定律发挥着关键作用。根据能量守恒定律，摆锤的初始动能等于其冲击试样后的动能加上试样吸收的能量。用数学语言表达，这个关系可以写成以下公式：

\\[ E_{\\text{initial}} = E_{\\text{final}} + E_{\\text{absorbed}} \\]

其中，\\( E_{\\text{initial}} \\) 是摆锤的初始动能，\\( E_{\\text{final}} \\) 是摆锤冲击试样后的动能，\\( E_{\\text{absorbed}} \\) 是试样吸收的能量。通过测量摆锤的摆幅，可以计算出 \\( E_{\\text{initial}} \\) 和 \\( E_{\\text{final}} \\)，进而求出 \\( E_{\\text{absorbed}} \\)。

摆锤冲击试验计算公式：从理论到实践

摆锤冲击试验计算公式，不仅仅是一个理论公式，更是一个实用的工具。在实际操作中，我们需要将理论公式转化为具体的计算步骤。以下是摆锤冲击试验计算公式的详细步骤：

1. 测量摆锤的初始高度：摆锤的初始高度决定了其初始势能。通常，摆锤的初始高度是固定的，但为了确保准确性，需要使用测量工具进行精确测量。

2. 测量摆锤的初始摆幅：摆锤的初始摆幅决定了其初始动能。通过使用角度测量工具，可以精确测量摆锤的初始摆幅。

3. 冲击试样：将摆锤从初始高度释放，冲击试样。观察摆锤冲击试样后的摆幅变化。

4. 测量摆锤的最终摆幅：摆锤冲击试样后，其摆幅会减小。通过使用角度测量工具，可以精确测量摆锤的最终摆幅。

5. 计算试样吸收的能量：根据能量守恒定律，试样吸收的能量等于摆锤的初始动能减去其冲击试样后的动能。具体计算公式如下：

\\[ E_{\\text{absorbed}} = \\frac{1}{2} m v_{\\text{initial}}^2 - \\frac{1}{2} m v_{\\text{final}}^2 \\]

其中，\\( m \\) 是摆锤的质量，\\( v_{\\text{initial}} \\) 是摆锤的初始速度，\\( v_{\\text{final}} \\) 是摆锤冲击试样后的速度。通过测量摆锤的摆幅，可以计算出 \\( v_{\\text{initial}} \\) 和 \\( v_{\\text{final}} \\)，进而求出 \\( E_{\\text{absorbed}} \\)。

摆锤冲击试验计算公式：影响因素与实际应用

摆锤冲击试验计算公式，看似简单，但在实际应用中，会受到多种因素的影响。了解这些影响因素，对于准确评估材料的冲击性能至关重要。

1. 摆锤的质量